DynamicX 视觉组学习笔记 - 基于分水岭算法的图像分割
在学习分水岭算法的时候我思考比较多的一个问题是为什么要用分水岭算法,就此次使用的示例图片来说,简单的色彩分割就可以得到所有向日葵花。但是简单的色彩分割达不到“识别出图片中较大的向日葵并标记”这种要求,色彩分割后的向日葵边缘是很清晰的,但是去除图片中较小的向日葵就会影响到目标向日葵的边缘,不去除较小向日葵就无法仅获得较大向日葵的边缘信息。分水岭算法在一定程度上解决了这个矛盾,在这里我们给出原图和边缘所在的大致范围,分水岭算法就可以得出较清晰的边缘。在实际操作中我花费最长时间解决的问题是最大的两个向日葵无法得到正确的边缘,原因是没��有标记已知背景导致分水岭算法将背景和向日葵分到了同一个区域,不知为什么网络上的一些例程没有标记背景。

理论基础
图像形态学
来源 数学形态学是以形态结构元素为基础对图像进行分析的数学工具。它的基本思想是用具有一定形态的结构元素去度量和提取图像中的对应形状以达到对图像分析和识别的目的。数学形态学的应用可以简化图像数据,保持它们基本的形状特征,并除去不相干的结构。数学形态学的基本运算有 4 个:膨胀、腐蚀、开启和闭合。它们在二值图像中和灰度图像中各有特点。基于这些基本运算还可以推导和组合成各种数学形态学实用算法。 在这里我仅用到了二值形态运算,基本的形态运算是腐蚀和膨胀,用 B(x)代表结构元素,对工作空间 E 中的每一点 x,腐蚀和膨胀的定义为:
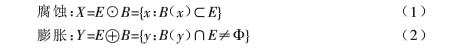
- 用 B(x)对 E 进行腐蚀的结果就是把结构元素 B 平移后使 B 包含于 E 的所有点构成的集合。
- 用 B(x)对 E 进行膨胀的结果就是把结构元素 B 平移后使 B 与 E 的交集非空的点构成的集合。
- ��先腐蚀后膨胀的过程称为开运算。它具有消除细小物体,在纤细处分离物体和平滑较大物体边界的作用。
- 先膨胀后腐蚀的过程称为闭运算。它具有填充物体内细小空洞,连接邻近物体和平滑边界的作用。
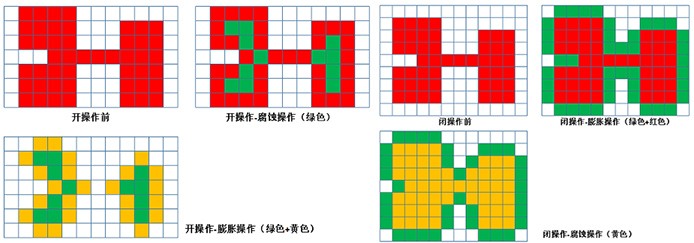
可见,二值形态膨胀与腐蚀可转化为集合的逻辑运算,算法简单,适于并行处理,且易于硬件实现,适于对二值图像进行图像分割、细化、抽取骨架、边缘提取、形状分析。但是,在不同的应用场合,结构元素的选择及其相应的处理算法是不一样的,对不同的目标图像需设计不同的结构元素和不同的处理算法。结构元素的大小、形状选择合适与否,将直接影响图像的形态运算结果。因此,很多学者结合自己的应用实际,提出了一系列的改进算法。如梁勇提出的用多方位形态学结构元素进行边缘检测算法既具有较好的边缘定位能力,又具有很好的噪声平滑能力。许超提出的以最短线段结构元素构造准圆结构元素或序列结构元素生成准圆结构元素相结合的设计方法,用于骨架的提取,可大大减少形态运算的计算量,并可同时满足尺度、平移及旋转相容性,适于对形状进行分析和描述。
距离变换
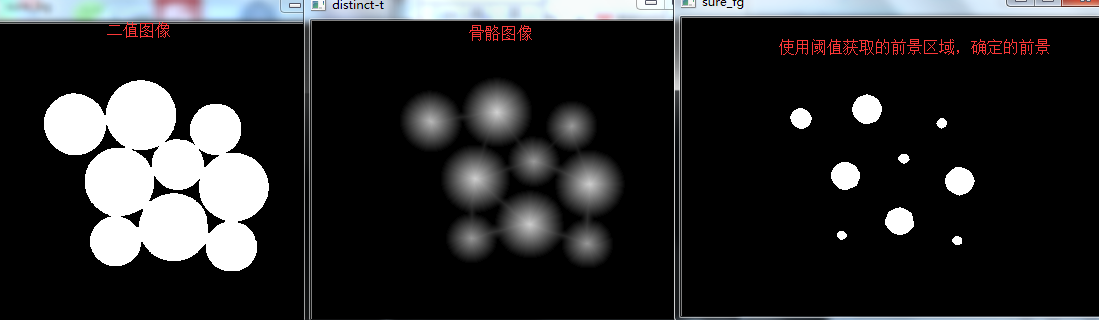
距离变换的处理图像通常都是二值图像,而二值图像其实就是把图像分为两部分,即背景和物体两部分,物体通常又称为前景目标。通常我们把前景目标的灰度值设为 255,即白色,背景的灰度值设为 0,即黑色。所以定义中的非零像素点即为前景目标,零像素点即�为背景。所以图像中前景目标中的像素点距离背景越远,那么距离就越大,如果我们用这个距离值替换像素值,那么新生成的图像中这个点越亮。 对距离变换后的图像进行适当的归一化处理就可以从一个二值图像中得到前景中心。
分水岭算法
有关算法的介绍,很多文章都指向了同一个来源。 分水岭算法主要用于图像分段,通常是把一副彩色图像灰度化,然后再求梯度图,最后在梯度图的基础上进行分水岭算法,求得分段图像的边缘线。对灰度图的地形学解释,我们我们考虑三类点:
- 局部最小值点,该点对应一个盆地的最低点,当我们在盆地里滴一滴水的时候,由于重力作用,水最终会汇聚到该点。注意:可能存在一个最小值面,该平面内的都是最小值点。
- 盆地的其它位置点,该位置滴的水滴会汇聚到局部最小点。
- 盆地的边缘点,是该盆地和其它盆地交接点,在该点滴一滴水,会等概率的流向任何一个盆地。
假设我们在盆地的最小值点,打一个洞,然后往盆地里面注水,并阻止两个盆地的水汇集,我们会在两个盆地的水汇集的时刻,在交接的边缘线上(也即分水岭线),建一个坝,来阻止两个盆地的水汇集成一片水域。这样图像就被分成 2 个像素集,一个是注水盆地像素集,一个是分水岭线像素集。
分水岭算法的整个过程:
- 把梯度图像中的所有像素按照灰度值进行分类,并设定一个测地距离阈值。
- 找到灰度值最小的像素点(默认标记为灰度值最低点),让 threshold 从最小值开始增长,这些点为起始点。
- 水平面在增长的过程中,会碰到周围的邻域像素,测量这些像素到起始点(灰度值最低点)的测地距离,如果小于设定阈值,则将这些像素淹没,否则在这些像素上设置大坝,这样就对这些邻域像素进行了分类。
- 随着水平面越来越高,会设置更多更高的大坝,直到灰度值的最大值,所有区域都在分水岭线上相遇,这些大坝就对整个图像像素的进行了分区。

在真实图像中,由于噪声点或者其它干扰因素的存在,使用分水岭算法常常存在过度分割的现象,这是因为很多很小的局部极值点的存在,这样的分割效果是毫无用处的。为了解决过度分割的问题,可以使用基于标记(mark)图像的分水岭算法,就是通过先验知识,来指导分水岭算法,以便获得更好的图像分段效果。通常的 mark 图像,都是在某个区域定义了一些灰度层级,在这个区域的洪水淹没过程中,水平面都是从定义的高度开始的,这样可以避免一些很小的噪声极值区域的分割。

OpenCV 实现的是基于标记的分水岭算法,所以在运行分水岭算法前需要通过预处理得到标记,标记是一个与待处理图像大小相同的矩阵,在数值上,零表示未知区域,正数表示注水点(数值相同表示互相连接),分水岭算法得到的边缘数值会被修改为-1。
分水岭算法让我联想到了图论中的网�络流和图像处理中的漫水填充(floodfill),同样都是抽象的流动算法,分水岭算法在流动的基础上增加了测地线这个概念,通过计算测地距离设置大坝来控制流动,达到了分类的目的。
代码实践
首先通过色彩分割得到大致的前景,然后通过形态学操作、距离变换得到确定的前景和后景生成标记,运行分水岭算法,在结果中寻找轮廓并标记外接矩形和坐标。
#include<opencv2/core.hpp>
#include<opencv2/highgui.hpp>
#include<opencv2/imgproc.hpp>
using namespace cv;
#include<iostream>
#include<string>
using namespace std;
Mat ColorExtract(Mat& src, Mat& mask) {
Mat bgr, hsv, dst;
//彩色图像的灰度值归一化
src.convertTo(bgr, CV_32FC3, 1.0 / 255, 0);
//颜色空间转换
cvtColor(bgr, hsv, COLOR_BGR2HSV);
//色相
int HMin = 0;
int HMax = 74;
//饱和度
int SMin = 0;
int SMax = 255;
//亮度
int VMin = 0;
int VMax = 255;
inRange(hsv,
Scalar(HMin, float(SMin) / 255, float(VMin) / 255),
Scalar(HMax, float(SMax) / 255, float(VMax) / 255),
mask);
//输出图像分配内存
dst = Mat::zeros(src.size(), CV_32FC3);
//只保留
for (int r = 0; r < bgr.rows; r++)
{
for (int c = 0; c < bgr.cols; c++)
{
if (mask.at<uchar>(r, c) == 255)
{
dst.at<Vec3f>(r, c) = bgr.at<Vec3f>(r, c);
}
}
}
dst.convertTo(dst, CV_8UC3, 255.0, 0);
return dst;
}
//分水岭算法
Mat WaterSegment(Mat src, Mat mask) {
Mat unknown_area = mask, sure_fg;
// 形态学膨胀
Mat kernel = getStructuringElement(MORPH_RECT, Size(9, 9));
dilate(unknown_area, unknown_area, kernel);
// 距离变换
distanceTransform(unknown_area, sure_fg, DIST_L2, DIST_MASK_3, 5);
sure_fg.convertTo(sure_fg, CV_8UC1);
// 将图像归一化
normalize(sure_fg, sure_fg, 0, 255, NORM_MINMAX);
// 转为二值图
threshold(sure_fg, sure_fg, 40, 255, THRESH_BINARY);
// 形态学闭操作,获得确定前景
morphologyEx(sure_fg, sure_fg, MORPH_CLOSE, kernel);
// 两次膨胀
Mat sure_bg = mask;
dilate(sure_bg, sure_bg, kernel, Point(-1,-1), 2);
// 二值化,获得确定背景,将确定背景标记为 1
threshold(sure_bg, sure_bg, 0, 1, THRESH_BINARY_INV);
Mat markers;
sure_bg.convertTo(markers, CV_32SC1);
// 使用findContours寻找marks并使用drawContours标记,前景标记从数字 2 开始
vector<vector<Point>> contours;
findContours(sure_fg, contours, RETR_TREE, CHAIN_APPROX_SIMPLE);
for (size_t i = 0; i < contours.size(); i++)
drawContours(markers, contours, static_cast<int>(i), Scalar::all(static_cast<int>(i + 2)), 2);
// 对原图做形态学腐蚀
Mat img;
kernel = getStructuringElement(MORPH_RECT, Size(3, 3));
morphologyEx(src, img, MORPH_ERODE, kernel);
// 调用opencv的分水岭算法
watershed(img, markers);
// 显示结果
Mat dst = Mat::zeros(markers.size(), CV_8UC3);
int index = 0, row = img.rows, col = img.cols;
for (int i = 0; i < row; i++) {
for (int j = 0; j < col; j++) {
index = markers.at<int>(i, j);
if (index == -1)
{
dst.at<Vec3b>(i, j) = Vec3b(255, 255, 255);
}
else {
dst.at<Vec3b>(i, j) = Vec3b(0, 0, 0);
}
}
}
return dst;
}
string GetCoordText(int x, int y){
stringstream text;
text<<"("<<x<<","<<y<<")";
return text.str();
}
void DrawBoundingRect(Mat& src, Mat mask) {
// 轮廓发现与绘制
cvtColor(mask,mask,CV_RGB2GRAY);
mask.convertTo(mask, CV_8UC1);
vector<vector<Point>> contours;
vector<Vec4i> hierarchy;
findContours(mask, contours, RETR_TREE, CHAIN_APPROX_SIMPLE);
for (size_t i = 0; i < contours.size();++i) {
// 最大外接轮廓
Rect rect = cv::boundingRect(contours[i]);
rectangle(src, rect, cv::Scalar(0, 0, 255), 2, LINE_8);
putText(src, GetCoordText(rect.x,rect.y), Point(rect.x, rect.y),
FONT_HERSHEY_SIMPLEX, 0.3, Scalar::all(255));
putText(src, GetCoordText(rect.x,rect.y+rect.height), Point(rect.x, rect.y+rect.height),
FONT_HERSHEY_SIMPLEX, 0.3, Scalar::all(255));
putText(src, GetCoordText(rect.x+rect.width,rect.y), Point(rect.x+rect.width, rect.y),
FONT_HERSHEY_SIMPLEX, 0.3, Scalar::all(255));
putText(src, GetCoordText(rect.x+rect.width,rect.y+rect.height), Point(rect.x+rect.width, rect.y+rect.height),
FONT_HERSHEY_SIMPLEX, 0.3, Scalar::all(255));
}
}
int main(int argc, char*argv[])
{
Mat img, mask, dst;
//输入图像
img = imread("input.jpg", IMREAD_COLOR);
if (!img.data || img.channels() != 3)
return -1;
dst = ColorExtract(img, mask);
dst = WaterSegment(img, mask);
DrawBoundingRect(img, dst);
imwrite("output.jpg", img);
waitKey(0);
return 0;
}
结果
