DynamicX 视觉组学习笔记 - 二维码定位与识别
这一次的任务简单来说就是二维码识别,只是要识别的不是 qr 码而是一个比较简单的自定义码。看过题目后我大致的想法是解决三个问题:
- 定位二维码
- 识别二维码
- 计数在同一张纸上的二维码
在这几个问题中我感觉最简单的应该是识别二维码,如果定位得到的图像足够理想那么识别的精准度也不会差,但是完成后我发现我把定位部分想得太复杂了。
理论基础
仿射变换与透视变换
仿射变换(Affine Transformation 或 Affine Map),又称为仿射映射,是指在几何中,图像进行从一个向量空间进行一次线性变换和一次平移,变换为到另一个向量空间的过程。仿射变换保持了二维图形的平直性和平行性。平直性:变换是直线的,变换后还是直线;平行性:二维图形之间的相对位置关系保持不变。

- 在几何中,任何变换都可以以矩阵乘法(线性变换)的形式表示,图像中的平移操作可以以矢量加法(平移)的形式表示;
- 一个任意的仿射变换都可以表示为乘以一个矩阵再加上一个向量的形式;[x, y]T 代表原始图像矩阵,是一个二维数组,x 代表像素的横坐标,y 代表像素的纵坐标;
- 如果线性变换矩阵 A=[[1, 0], [0,1]],那么 A 点乘矩阵[x, y]T 就不会改变[x, y]T 的信息,此时,仿射变换就变成了平移操作,移动的行列值就是矩阵 B 中的元素值;
- 如果线性矩阵 A=[[cosθ, -sinθ], [sinθ, cosθ]],那么线性变换就变成了图片的旋转操作,旋转角度θ。矩阵 B 代表旋转中心的坐标偏移量。
由于这次任务的识别材料是一个不断运动的视频,由于视角、畸变等原因拍摄出来的二维码并不是平直的,所以仅使用仿射变换并不能得到理想的图像。
透视变换(Perspective Transformation)就是将图片投影到一个新的视平面,也称为投影映射。相对仿射变换来说,改变了直线之间的平行关系。
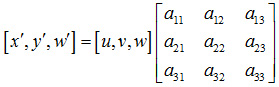
- 在 3*3 的变换矩阵 M 中,包含了线性变换矩阵和平移矩阵,因此,仿射变换可以看作透视变换的一种特殊形式;
- 经过透视变换后的图片通常不是平行四边形(除非映射平面和原平面平行);
- 求取转换矩阵时,需要四个点的坐标,同时要保证至少三个不在同一直线;
- 已知 4 个点的坐标和想要变换成的矩阵坐标,即可求出 3*3 的变换矩阵。
虽然说经过透视变换的图像一般不是平行四边形,但在这次的任务中我使用透视变换将不平行的图像转换成正方形以便识别。
多边形拟合
关于多边形拟合的算法我起初并没有去了解,是经过了师兄提醒才仔细查找了实现原理。
opencv 中的多边形拟合函数使用道格拉斯-普克算法(Douglas-Peucker)来实现,算法过程描述如下:
- 在曲线首尾两点 A,B 之间连接一条直线 AB,该直线为曲线的弦;
- 得到曲线上离该直线段距离最大的点 C,计算其与 AB 的距离 d;
- 比较该距离与预先给定的阈值 threshold 的大小,如果小于 threshold,则该直线段作为曲线的近似,该段曲线处理完毕。
- 如果距离大于阈值,则用 C 将曲线分为两段 AC 和 BC,并分别对两段取信进行 1~3 的处理。
- 当所有曲线都处理完毕时,依次连接各个分割点形成的折线,即可以作为曲线的近似。
对于一个畸变不严重的平行四边形来说通过道格拉斯-普克算法获得的前四个点可以近似当作四个顶点。而在实践中我由于担心拟合效果不够理想所以使用了一个更加复杂的方式实现。
霍夫直线检测
霍夫直线检测(Hough Line Detection)的基本原理在于利用点与线的对偶性,即图像空间中的直线与参数空间中的点是一一对应的,参数空间中的直线与图像空间中的点也是一一对应的。这意味着我们可以得出两个非常有用的结论:
- 图像空间中的每条直线在参数空间中都对应着单独一个点来表示;
- 图像空间中的直线上任何一部分线段在参数空间对应的是同一个点。
因此霍夫直线检测算法就是把在图像空间中的直线检测问题转换到参数空间中对点的检测问题,通过在参数空间里寻找峰值来完成直线检测任务。
这里所说的参数空间就是与 x-y 直角坐标对应的 k-b 直角坐标,在 x-y 坐标中过一点的所有直线可以描述为 k-b 坐标中的一条直线;而 x-y 中的两点连线就可以表示为 k-b 坐标中的两线交点,在将 x-y 坐标中的点集转换到 k-b 坐标中后求峰值交点就可以得到过最多点的直线,也就达到了直线检测的目的。
而实际上由于直角参数空间的局限性,霍夫直线检测采用的是极坐标参数空间,在 OpenCV 的实现中还存在概率霍夫直线检测这个变体,相关原理就更复杂了。
代码实践
视频流的处理
视频经过解码得到的每一帧就是一张图片,在这里我直接使用 OpenCV 的函数通过流输入获得每一帧并进行处理。每帧的处理用时大约为 0.1 秒。
int main() {
VideoCapture cap;
cap.open("input.mp4");
Mat frame;
cap >> frame;
puts("loop start");
while (!frame.empty()) {
clock_t start = clock();
Mat dst = process(frame);
clock_t end = clock();
putText(dst, "process for "+to_string((double)(end - start) / CLOCKS_PER_SEC)+" second", Point(10, 20),
FONT_HERSHEY_SIMPLEX, 0.5, Scalar::all(0));
imshow("dst",dst);
cap >> frame;
waitKey(1000/30);
}
return 0;
}
定位二维码
首先是与之前任务类似的预处理过程,对图像进行降噪形态学等处理后得到二值图,然后查找边缘以待筛选。 后面的筛选并获得顶点的过程是花费我比较多时间的一项工作,在第一版实现中我首先对边缘逐个进行多边形拟合,对拟合得到的点不超过 10 个的结果进行尺寸和边长筛选,再将筛选出的边缘进行霍夫直线检测获得四条直线计算四个顶点。这个方法执行效率很低并且识别率不够高,主要耗时在霍夫直线检测。第二版实现中我去除了霍夫直线检测的部分,通过调整参数控制多边形拟合的结果为四个点,经过边长筛选后就作为筛选结果等待识别。从肉眼观察来看,后一种方式得出的顶点并没有前一种方式得出的顶点准确,切出的二维码有明显晃动,但执行效率和识别率都提升了很多。 在两种实现中我都发现固定参数很难兼顾视频里的每一帧图像,又因为参数和结果的数值关系是单调的,所以我采用了二分法调整参数,效果有显著提升。
//查找轮廓
vector<vector<Point>> contours;
vector<Vec4i> hierarchy;
findContours(close, contours, hierarchy, CV_RETR_TREE, CHAIN_APPROX_NONE);
//查找二维码并计数
vector<size_t> maybeSqares;
vector<vector<Point>> corners;
float epsilon;
for(size_t i = 0; i < contours.size(); i++) {
for(size_t k = 30, j = 9, mid = 20; k > j; mid = (k+j)/2+1) {// 二分求参
vector<Point> approx;
epsilon = (0.001 * mid) * arcLength(contours[i], true);
approxPolyDP(Mat(contours[i]), approx, epsilon, true);
if(approx.size() < 4) {
k = mid - 1;
}else if(approx.size() > 4) {
j = mid;
}else if(hierarchy[i][3] >= 0 && approxSqare(approx)) { // 子轮廓较稳定,父轮廓不稳定
maybeSqares.push_back(i);
corners.push_back(approx);
drawContours(dst, corners, corners.size()-1, Scalar(0, 0, 255), 2);
break;
}else{
k = mid - 1;
}
}
}
识别二维码
这部分实现比较顺利,按照上一步得出的顶点将二维码从原图变换为正方形,对每个块的颜色求均值,筛掉外边框不是黑色和全部是黑色的,剩下的就是确定的二维码。
bool getSqareColor(Mat src, Rect rec) {
Mat mask = Mat::zeros(src.size(), CV_8UC1);
rectangle(mask, Point(rec.x,rec.y), Point(rec.x+rec.width, rec.y+rec.height), Scalar(255), -1);
return mean(src, mask)[0] > 127;
}
String getCode(Mat src, vector<Point2f> from) {
if(from.size() != 4) return "";
Mat dst = Mat::zeros(480, 480, CV_8UC1);
vector<Point2f> to{Point(0,0), Point(480, 0), Point(0, 480), Point(480, 480)};
warpPerspective(src, dst, getPerspectiveTransform(from, to), dst.size(), INTER_LINEAR);
bool colors[6][6];
for(size_t i = 0; i < 6; i++){ // 获取颜色
for(size_t j = 0; j < 6; j++){
colors[i][j] = getSqareColor(dst, Rect(i*80, j*80, 80, 80));
}
}
for(size_t i = 0; i < 6; i++) // 外边框筛选
if(colors[i][0] || colors[i][5] || colors[0][i] || colors[5][i])
return "";
String res = "";
for(size_t i = 0; i < 6; i++){ // 转字符串
int sum = 0;
for(size_t j = 0; j < 6; j++)
if(colors[j][i]) sum += 1;
res += to_string(sum);
}
if(res == "000000")
return "";
else return res;
}
计数在同一张纸上的二维码
这里我首先尝试的是从二值图中删去识别到的二维码之后进行连通图检测,然后通过二维码中点位置的结果确定在同一连通图中的二维码。在实际操作中这个思路受到了两个问题的影响无法实现,一是即使经过强降噪图像中仍有大量噪点,二是连通图检测一般仅考虑四连通或八连通的情况,对于照片来说过于微观,容错性差。 后来的实现方式是从二值图中删去识别到的二维码之后进行轮廓查找,然后遍历轮廓确定每个二维码的中心是否在该轮廓内并计数。这种方式在测试视频中表现良好,但是如果二维码外存在多层轮廓就需要再增加颜色和距离的判断。
//计算前缀
Mat noCodeImg = shold.clone();
for(size_t i = 0; i < sqares.size(); i++) {
drawContours(noCodeImg, contours, maybeSqares[sqares[i]], Scalar::all(255), -1);
drawContours(noCodeImg, contours, maybeSqares[sqares[i]], Scalar::all(255), 1);
}
vector<vector<Point>> noCodeContours;
findContours(noCodeImg, noCodeContours, CV_RETR_LIST, CHAIN_APPROX_NONE);
vector<size_t> blockCount(noCodeContours.size()); // 该轮廓内有几个
vector<size_t> blockNumber(sqares.size()); // 属于哪个轮廓
imshow("noCode", noCodeImg);
for(size_t i = 0; i < sqares.size(); i++) {
for(size_t j = 0; j < noCodeContours.size(); j++) {
Point center(0, 0);
for(int k = 0; k < corners[sqares[i]].size(); k++)
center += corners[sqares[i]][k];
center *= (1. / corners[sqares[i]].size());
if(pointPolygonTest(noCodeContours[j], center, false) > 0) {
blockNumber[i] = j+1;
blockCount[j] += 1;
break;
}
}
}
结果
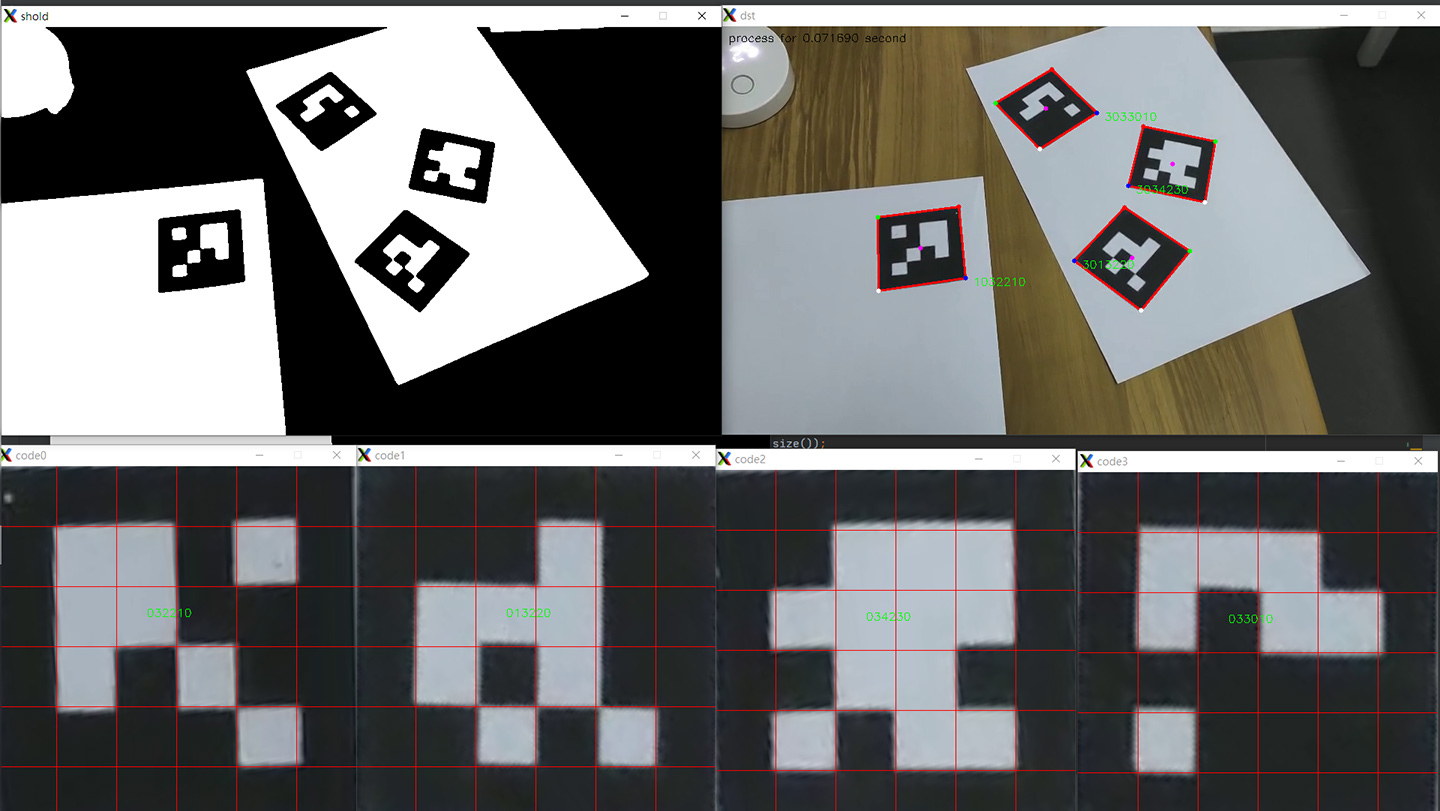
测试视频的难度比较低,几个二维码处于光线充足的室内,并且大小相差不多,背景的颜色也很纯净。有一个没有解决的问题是在视频中间部分有几秒遮住了一个二维码的一角导致无法定位,我尝试为视频每一帧都增加一个外边框来扩展图像范围,但结果是由于在定位阶段使用了多边形趋近获得顶点,这种方法无法获得不存在在图像上的点,所以没有成功。我认为还是需要使用霍夫直线检测或其他算法才能获得缺失的顶点位置。可见,目前的代码很难应对光线变化、反光、彩色、不同尺寸等干扰。 下面是某一帧的截图,左上 shold 窗口为预处理得到的二值图,右上 dst 窗口为原图(左上角标明了当前帧的处理用时,红色框为二维码定位得到的边框,彩色点为顶点和中点,绿色字为识别得到的码),下面四个 code 窗口为各个二维码变换后得到的图像。